AcademiaFMB

Valor de P, nível de significância estatística e poder estatístico são termos essenciais na pesquisa e análise de artigos científicos. Esse artigo tentará tornar esses conceitos-chave da bioestatística mais compreensíveis.

Existem pessoas que gostam de lidar com números e sentem uma maior facilidade ao estudarem bioestatística. Infelizmente, eu não me incluo nesse grupo. Desde o meu primeiro contato com bioestatística e alguns dos seus companheiros, vulgo valor de P, nível de significância estatística e poder estatístico, senti uma enorme dificuldade em compreender esses conceitos. Tentava ler diferentes materiais, assistia a diferentes aulas e, mesmo assim, continuava confusa. Cada vez que parecia que eu estava começando a entender algo, logo percebia que minha compreensão estava equivocada.

Caro leitor, não se preocupe se achar esses tópicos difíceis, pois eles são, de fato, complexos. No entanto, resolvi escrever esse artigo com o intuito de apresentar esses conceitos de uma maneira mais acessível e tentar ajudar aqueles que, da mesma forma que eu, possuem alguma dificuldade em entender alguns conceitos bioestatísticos. Digamos que estou escrevendo esse texto pensando que, se meu eu do passado o tivesse lido, as coisas seriam facilitadas.

Iniciando o caminho das pedras

Vamos imaginar que você é um pesquisador interessado em avaliar se o uso regular do medicamento X pode levar a uma redução na pressão arterial em pacientes com hipertensão. Com base nisso, você, um pesquisador que assistiu algumas sessões da LAC, formula sua hipótese da seguinte maneira: 

“A administração regular do medicamento X resultará em uma redução significativa da pressão arterial em pacientes com hipertensão, em comparação com o grupo controle que recebeu placebo.”

Figura 1

Fonte: Mufid Majnun

#PraCegoVer A imagem mostra uma pessoa com o braço esticado em cima de uma mesa enquanto um aparelho afere sua pressão.

Precisamos ter em mente, então, que, nesse cenário: 

• A variável independente é o medicamento X (Conhecida como a intervenção, é a variável que você acredita ter um efeito sobre a outra variável)
• A variável dependente é a redução da pressão arterial (Conhecida como desfecho, é afetada pela variável independente.)
• O grupo de intervenção desse estudo = o grupo que tomará o medicamento X
• O grupo controle desse estudo = o grupo que não tomará o medicamento X.

Importante falar que, ao iniciar a formulação de uma pergunta de pesquisa, é essencial resumir os principais elementos que serão investigados em uma hipótese de pesquisa. Em outras palavras, é necessário explicitar a variável independente e a variável de dependente em uma única frase, produzida antes do início da pesquisa, para resumir o que se pretende testar. 

Com isso em mente e com a hipótese do estudo estabelecida, entram em cena dois novos protagonistas: a hipótese nula e a hipótese alternativa. 

Pense na hipótese nula como aquela pessoa que está sempre pronta para discordar de tudo o que você diz. No caso, a hipótese nula vem justamente para negar a hipótese que você gerou, afirmando que não existem diferenças entre os resultados do grupo que tomou o medicamento (grupo de intervenção) e o grupo controle. Logo, se não existe diferença entre os grupos (o grupo de intervenção e o grupo controle possuem resultados aproximados), significa dizer que não há evidência estatística suficiente para acreditar que o medicamento funciona.

A hipótese nula é sempre pressuposta como verdadeira até o momento que possa ser rejeitada por um teste estatístico.

Por outro lado, a hipótese alternativa é o oposto, ela sugere que há, de fato, diferenças entre esses dois grupos e portanto, no nosso caso,  há evidência estatística suficiente para dizer que muito provavelmente o medicamento funciona.

Um ponto importante é que a hipótese alternativa não tem como ser testada diretamente, por isso, ela só é aceita caso o teste de significância estatística rejeite a hipótese nula.

Em resumo, no caso da nossa hipótese inicial, teríamos:

Hipótese Nula (H0): A administração regular do medicamento X não resultará em uma redução significativa da pressão arterial em pacientes com hipertensão, em comparação com o grupo controle que recebeu placebo. 

Hipótese Alternativa (Ha): A administração regular do medicamento X resultará em uma redução significativa da pressão arterial em pacientes com hipertensão, em comparação com o grupo controle que recebeu placebo.

VALOR DE P

Nos estudos, normalmente busca-se um valor de P < 0,05 (menor que 5%) como ideal, e quanto menor esse valor, melhor!

“Mas o que é esse valor de P, afinal?" 

O valor de P representa a probabilidade de obter um resultado pelo menos tão extremo quanto o observado, sob a suposição de que a hipótese nula é verdadeira.

"Certo, entendi, mas ainda não compreendi..." 

Em outras palavras, o valor de P representa a probabilidade de obter um dado resultado, assumindo que os grupos (de intervenção e controle) são iguais (hipótese nula verdadeira). 

Ora, se a hipótese nula for verdadeira e, portanto, os grupos são iguais, então a diferença observada entre meus grupos só pode ser devida ao acaso.

Por isso, enquanto pesquisador, eu quero que o valor de P seja < 0.05, visto que, se ele for pequeno, isso significa que é muito improvável que a diferença encontrada tenha sido fruto do acaso e, portanto, podemos assumir que é, também, muito improvável que os grupos sejam iguais. Assim, minha hipótese nula pode ser rejeitada.

É como se o valor de P menor que 0.05 nos dissesse que a chance de os grupos serem iguais e termos encontrado o resultado ao acaso é muito pequena, então provavelmente existe uma diferença causada por algo, como o medicamento X em nosso exemplo. 

Portanto, quanto menor o valor de P, menor a probabilidade de que o resultado seja devido ao acaso e, por outro lado, maior a probabilidade de que o resultado esteja relacionado a outra intervenção, como o medicamento X em nosso caso. 

TESTE DE HIPÓTESES  

Teste de hipóteses é basicamente uma forma por meio da qual definimos se vale a pena rejeitar a hipótese nula em favor da hipótese alternativa.

O quadro do teste de hipóteses é uma ferramenta utilizada para tomar decisões estatísticas com base nos resultados obtidos em um teste de hipóteses. 

Nesse sentido, quando tratamos sobre a possibilidade de rejeitar ou não a hipótese nula, utilizamos o quadro de possibilidades para analisar:

1. Quando rejeitamos uma hipótese nula falsa. 
2. Quando não rejeitamos uma hipótese nula verdadeira. 
3. Quando rejeitamos uma hipótese nula verdadeira. 
4. Quando não rejeitamos uma hipótese nula falsa. 

Os dois primeiros cenários estão corretos, os dois últimos incorretos. Dentre os cenários incorretos, o terceiro corresponde ao erro tipo 1 e o quarto corresponde ao erro tipo 2.

Figura 2

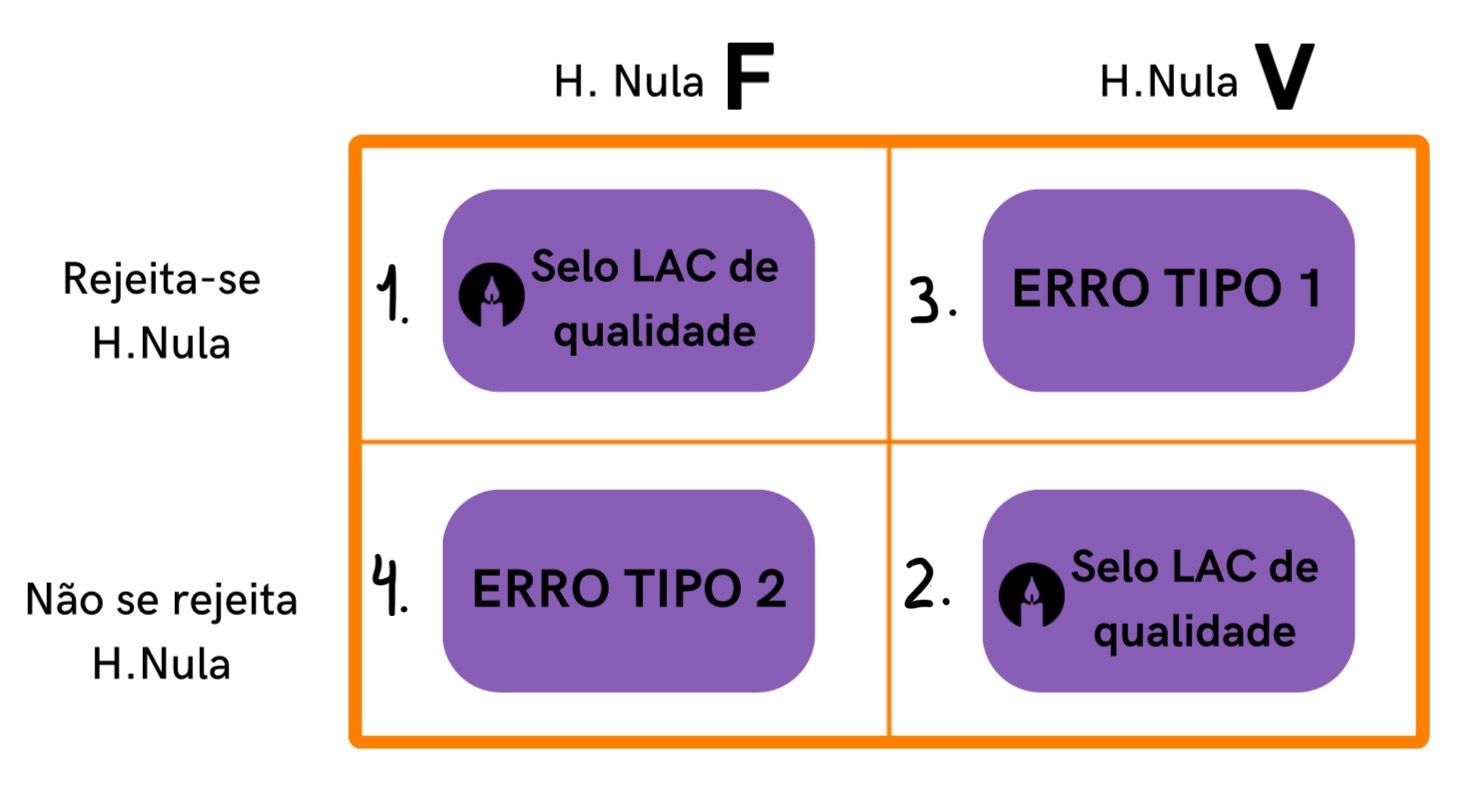
Fonte: produzida pela autora

#Pracegover uma quadro 2x2 expondo as quatros possibilidades citadas acima

O que precisa ficar claro para você é:

Quando ocorre o erro tipo 1, o estudo diz “olha, existe diferença entre os grupos”, quando, na realidade, essa diferença não existe. Temos, portanto, um falso positivo.

Já quando ocorre o erro tipo 2, o estudo diz “olha, NÃO existe diferença entre os grupos”, quando, na realidade, essa diferença existe. Temos, portanto, um falso negativo.

Erro tipo I, Alfa / Nível de Significância Estatística 

Alfa, também conhecido como nível de significância estatística, é o nome que damos à probabilidade de ocorrer o erro tipo 1 em um estudo. Ou seja, é a probabilidade do estudo erroneamente rejeitar a hipótese nula (ao afirmar que há uma diferença entre os grupos) quando, na realidade, a hipótese nula é verdadeira (não há diferença real). 

No caso do nosso exemplo, o erro do tipo 1 nos levaria a acreditar erroneamente que o medicamento X é eficaz na redução da pressão arterial em indivíduos com hipertensão, quando, na verdade, ele não possui eficácia real.

O nível de significância estatística diz o quão rigoroso serei ao considerar evidências para rejeitar a hipótese nula. Um alfa de 0,05 implica que você está disposto a aceitar uma probabilidade de 5% de cometer um erro do Tipo 1.

Quanto mais baixa for a probabilidade de um erro tipo 1, mais rigoroso e criterioso se torna o estudo em afirmar que há uma diferença. Em outras palavras, o estudo só aponta uma diferença quando houver uma alta probabilidade dessa diferença ser real.

Erro tipo II, Beta e Poder Estatístico 

Beta é o nome que damos à probabilidade de ocorrer o erro tipo 2 em um estudo. Em outras palavras, é a probabilidade de o estudo não conseguir detectar uma diferença real entre os grupos quando, na realidade, essa diferença existe. Através do valor (1-Beta), obtemos o poder estatístico do estudo. Podemos analisar da seguinte forma: quanto menor o valor de beta (probabilidade de ocorrer o erro tipo 2), maior o poder estatístico do estudo. 

No caso do nosso exemplo, o erro do tipo 2 nos levaria a erroneamente concluir que o medicamento X não é eficaz na redução da pressão arterial em indivíduos com hipertensão, quando, na verdade, ele é eficaz.

O poder estatístico vai justamente representar a capacidade do estudo de detectar uma diferença real, caso ela exista. Imagine que os estudos com alto poder estatístico são como olhos de águia que podem detectar a presa (a diferença entre os grupos) mesmo quando ela é pequena. 

Logo, quando tenho um estudo com alto poder estatístico, consigo identificar até mesmo pequenas diferenças entre os grupos. Isso resulta na diminuição da probabilidade de cometer o erro do tipo 2, já que ele ocorre quando erroneamente concluímos que não há diferença quando, na realidade, ela existe.

Uma forma de aumentar o poder estatístico de um estudo é aumentando minha amostra, o que nem sempre é possível de ser feito, uma vez que exige maior investimento de dinheiro, tempo (para coletar os dados) e uma maior complexidade estatística, por exemplo.

Fim da jornada 

Espero que os termos bioestatísticos tenham passado a fazer um maior sentido após esse texto. Caso tenha ficado qualquer dúvida, só deixar um comentário que responderemos.

Referências:

FREGNI, Felipe; ILLIGENS, Ben M. W. Critical Thinking in Clinical Research: Applied Theory and Practice Using Case Studies. Oxford University Press, 2018. p. 1-669.

HULLEY, Stephen B; CUMMINGS, Steven R; BROWNER, Warren S; GRADY, Deborah G; NEWMAN, Thomas B. Delineando a Pesquisa Clínica. 4 ed. Porto Alegre: Artmed, 2015.

Fletcher, Robert H, and Suzanne W Fletcher. Epidemiologia Clínica : Elementos Essenciais. Porto Alegre, Artmed, 2006.

TOIGO, A. O que é erro tipo 1 e 2 em estatística? [Epidemiologia]. Disponível em: <https://youtu.be/Iod1o00madE?si=KYQzOSD_oqgQ2BIq>. Acesso em: 10 out.2023.